Schnorr y BLS: dos propuestas para mejorar la criptografía de Bitcoin

Las firmas digitales se parecen a las firmas reales en que ambas permiten probar que el emisor de un mensaje es quien dice ser. Dentro del ámbito de la blockchain, la firma digital sirve para probar que un mensaje proviene de una persona específica y no, por ejemplo, de un hacker.

Para la firma de las transacciones en Bitcoin se escogió un algoritmo de firma digital (DSA, por sus siglas en inglés) denominado ECDSA (Elliptic Curve Digital Signature Algorithm), pues emplea una curva elíptica como herramienta para generar una clave pública a partir de una clave privada, lo que permite firmar mensajes y transacciones, de modo que terceras partes pueden comprobar la autenticidad de la firma, mientras que el firmante conserva la capacidad de crear la firma.

Con ECDSA, las operaciones aritméticas son realizadas sobre la curva. Por ejemplo, para sumar P + Q, se obtiene primero el punto -R, en la intersección de la prolongación del segmento PQ con la curva elíptica. El punto resultante de la suma es R, el reflejo de -R, como se ve en la gráfica siguiente:

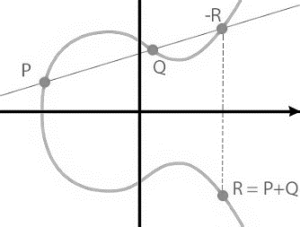
Si suponemos que el punto Q se mueve hacia P, cuando este coincida con P, tendremos una recta tangente a la curva, que pasa por P. En ese caso el valor resultante de R será:

R= P+P=2P

En el ejemplo siguiente, donde se escoge un punto generador G, se usa la técnica de la tangente tres veces consecutivas, para obtener el punto 8G:

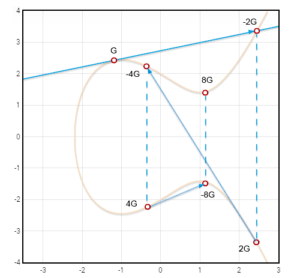
Quien conoce la clave privada y realiza este ciclo una gran número de veces, obtiene la clave pública -por ejemplo, la coordenada x del punto resultante- de manera relativamente sencilla, pero el proceso inverso no puede reconstruirse si no se conoce el número de pasos realizados. Es decir, no se puede saber cuál fue el punto generador de un punto determinado de la curva.

ECSDA cumple con su cometido de garantizar las transacciones entre pares, pero hay capacidades que no tiene, como por ejemplo la integración de múltiples firmas en una sola firma.

Las firmas digitales Schnorr y otra propuesta más reciente de Boneh-Lynn-Shacham, a breviada como BLS, permiten el manejo de múltiples firmas digitales, entre otras ventajas frente a ECDSA.

Ventajas de las firmas Schnorr

Las firmas Schnorr tienen un tamaño constante que es independiente del número de participantes en el esquema de múltiples firmas. Por esta razón el rendimiento de este esquema mejora sustancialmente al evitar el requerimiento de validad cada firma por separado. Además, la verificación de las firmas Schnorr es ligeramente más rápida que las de ECDSA.

Varios autores coinciden en afirmar que el método de Schnorr era el mejor en el momento en que se publica el Libro Blanco del Bitcoin, pero no fue seleccionado ya que estaba patentado en ese momento. Justamente es objeto de discusión en estos momentos ya que la patente venció.

En Bitcoincore.org, el portal web del grupo principal de desarrolladores de Bitcoin, se expone en este documento el funcionamiento de las firmas Schnorr y los beneficios que ofrecen en comparación con ECDSA.

El reemplazo del algoritmo de firma digital (ECDSA) por el más eficiente algoritmo Schnorr ha estado en el tope de las mejoras deseadas de muchos desarrolladores de Bitcoin. Un algoritmo simple que mejora la criptografía de curva elíptica, Schnorr habilita varias mejoras del esquema actual, mientras preserva todas sus características y supuestos de seguridad… Especialmente, las firmas Schnorr trabajan con «multifirmas nativas», lo que permite la agregación de múltiples firmas en una sola que es la suma de las claves de sus respectivas entradas.

Bitcoin Core

Desde el punto de vista de la privacidad, Schnorr tiene puntos a favor: no permite distinguir entre una multi-firma y una firma convencional, ni es posible determinar cuál de los participantes autorizó la transacción.

Entre las limitaciones de las firmas Schnorr, el proceso de la agregación de firmas emplea un generador de números al azar, lo cual es considerado inseguro respecto a la escogencia determinística que emplea ECDSA. También el esquema de múltiples firmas requiere dos rondas de comunicación, algo que puede ser problemático cuando se trabaja con carteras frías.

Firmas BLS

Las firmas BLS, por su parte, resuelven estas y otras limitaciones de las firmas Schnorr y además son dos veces más cortas que las de Schnorr o ECDSA. Uno de los co-autores de BLS, Dan Boneh, explica cómo se genera esa firma digital: en vez de realizar un hash del mensaje y usar ese hash en el algoritmo de firma como un número, como se hace en ECDSA y en Schnorr, en BLS el hash del mensaje se toma como la coordenada x del punto de la curva H(m).

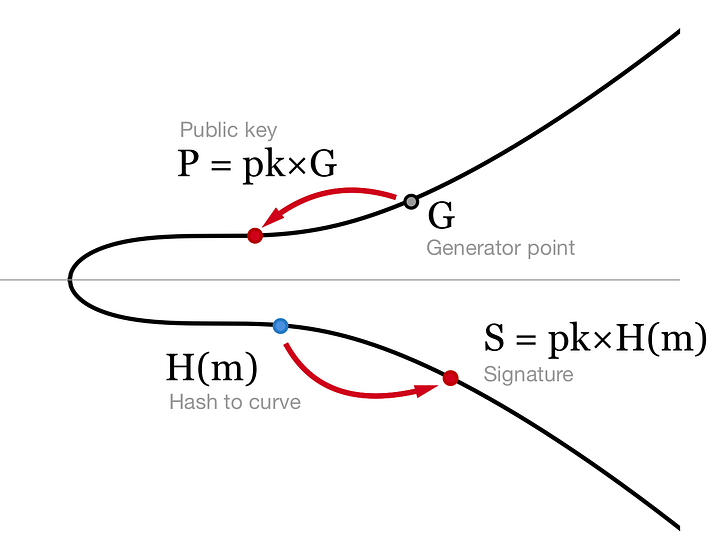
La firma S se obtiene multiplicando la clave privada por H(m). La firma es entonces un punto en la curva y toma 33 bytes en formato comprimido. La curva elíptica no es la misma que usa ECDSA, tiene otros parámetros.

A pesar de las ventajas de BLS, hay al parecer acuerdo entre los principales desarrolladores de Bitcoin en sustituir ECDSA por Snhnorr, de acuerdo a este Tweet: